A System Theoretic Fable
in which
Serious Misunderstandings Occur among
Systems Engineers
A. Wayne Wymore, Ph.D.
Professor of Systems & Industrial Engineering, Emeritus,
The University of Arizona
4301 North Camino Kino
Tucson AZ 85718-6657, USA
phone: 520 299 6663
e-mail: wayne@sie.arizona.edu
Abstract
(P.0) This paper was motivated by a pedagogical experience provided by a course offered in the Department of Systems and Industrial Engineering at the University of Arizona in the Fall of 1997. The paper focuses on two classroom exercises assigned to students in the class but is presented as a system theoretic fable reflecting, in many aspects, a typical American engineering experience in which serious misunderstandings occur among engineers attempting to design a system. The confusion arises from the definition and specification of functional system designs and the implementation of functional system designs by buildable system designs.
As a byproduct of the analysis of student responses to these assignments, new system theoretic results were developed and are reported here:
a theorem at (P.15) characterizing a class of systems that are "universal" implementations or simulators,
an example at (P.29) that shows that an implementable system design may not implement every functional system design in the functionality space,
a theorem at (P.34) that asserts that if one system is a state-homomorphic image of another system, then the systems have identical I/O behavior with respect to initial states,
an example at (P.36) that shows that two systems may have identical I/O behavior with respect to initial states, but do not necessarily have a homomorphic relationship,
a theorem at (P.44) that asserts that if two systems have identical I/O behavior with respect to initial states, then they have isomorphic minimizations.
Introduction.
(P.1) University of Arizona students registered in the course SIE554, Concurrent Engineering and System Design, a.k.a. Model-Based Systems Engineering, in the Fall of 97, were assigned to one of six teams and the teams were given weekly assignments among which were two, similar to the following:
first, find a functional system design to satisfy the I/O requirement IORx12 (MBSE, page 661) for the design of a system to process an input stream of 0’s and 1’s and to output a 1 if and only if the system recognizes the pattern 0, 1, 1, 1, 0 in the input stream, and
second, implement the functional system design with a system design buildable in the technology TYRx2 (the set of all system models with exactly two states such that every input port and output port has exactly two elements; see MBSE, page 681.)
The I/O requirement
IORx12
(P.2) IORx12 = (OLRx12, IRx12, ITRx12, ORx12, OTRx12, ERx12) where
OLRx12 = NND, (* TSRx12 = IJS++. *)
IRx12 = {0, 1},
ITRx12 = FNS(TSRx12, IRx12),
ORx12 = {0, 1},
OTRx12 = {g: g .E. FNS(TSRx12, ORx12); there exists f .E. ITRx12 such that, for t .E. TSRx12[5, NND), g(t) = 1 if and only if f(t - 5) = 0,
f(t - 4) = 1, f(t - 3) = 1, f(t - 2) = 1, f(t - 1) = 0},
ERx12 = {(f, G): f .E. ITRx12; G .S. OTRx12;
G = {g: g .E. .FNS(TSRx12, ORx12);
if t .E. TSRx12[5, NND), then g(t)
= 1, if f(t - 5) = 0, f(t - 4) = 1, f(t - 3) = 1,
f(t - 2) = 1, f(t - 1) = 0,
= 0, otherwise}}.
The eligibility function ERx12 says that a system that satisfies IORx12 shall output a 1 if and only if the previous 5 inputs were in the pattern 0, 1, 1, 1, 0, otherwise the system shall output 0.
(P.3) IORx12 is an I/O Requirement.
Proof:
That IORx12 .E. IOSPECS is a consequence of the following 6 observations/deductions corresponding to the conditions required by the definition at MBSE(6.5):
(i) OLRx12 = NND
.E. IJS+ È {NND}.
(ii) IRx12 = {0, 1} is a set not empty,
(iii) ITRx12 = FNS(TSRx12, IRx12) is a subset not empty of FNS(TSRx12, IRx12) where TSRx12 = IJS[0, OLRx12),
(iv) ORx12 = {0, 1} is a set not empty,
(v) OTRx12 is a subset of FNS(TSRx12, ORx12), by definition; if f = CNS0, then g = CNS0 .E. OTRx12, so OTRx12 <> {}.
(vi) That ERx12 is a function defined over the set ITRx12 with values in the set of nonempty subsets of OTRx12 is a consequence of the following 3 observations/deductions corresponding to the conditions required by the definition at MBSE(A1.155):
(i) It must be shown that ERx12 .S. ITRx12 >< (.PS.OTRx12 - {{}}). If (f, G) .E. ERx12, then, by the definition of ERx12, f .E. ITRx12 and G .S. OTRx12, by the definition of OTRx12. Hence, ERx12 .S. ITRx12 >< .PS.OTRx12. To show that G <> {}, let g be defined as follows: For t .E. TSRx12, g(t)
= 0, if t .E. TSRx12[0, 5);
= 1, if t .E. TSRx12[5, NND) and f(t - 5) = 0, f(t - 4) = 1,
f(t - 3) = 1, f(t - 2) = 1, f(t - 1) = 0;
= 0, if t .E. TSRx12[5, NND) and not f(t - 5) = 0, f(t - 4) = 1,
f(t - 3) = 1, f(t - 2) = 1, f(t - 1) = 0.
Then, g .E. OTRx12, g .E. ERx12(f) and ERx12(f) <> {}.
(ii) It must be shown that for every f .E. ITRx12, there exists G .S. OTRx12 such that G <> {} and (f, G) .E. ERx12. If f .E. ITRx12 and G
= {g: g .E. . FNS(TSRx12, ORx12); if t .E. TSRx12[5, NND), then g(t)
= 1, if f(t - 5) = 0, f(t - 4) = 1, f(t - 3) = 1,
f(t - 2) = 1, f(t - 1) = 0,
= 0, otherwise},
then, as above, G <> {} and (f, G) .E. ERx12.
(iii) It must be shown that ERx12 is single-valued. If {(f1, G1), (f2, G2)} .S. ERx12 and f1 = f2, and g .E. G1, then, for t .E. TSRx12[5, NND), g(t)
= 1, if and only if f1(t - 5) = 0, f1(t - 4) = 1, f1(t - 3) = 1,
f1(t - 2) = 1, f1(t - 1) = 0,
= 1, if and only if f2(t - 5) = 0, f2(t - 4) = 1, f2(t - 3) = 1,
f2(t - 2) = 1, f2(t - 1) = 0.
Hence, g .E. G1 if and only if g .E. G2. Hence, G1 = G2.
Finally, by the definition at MBSE(6.5), it must be shown that OTRx12 = .U.RNG(ERx12). To this end consider the following deductions: g .E. OTRx12
if and only if
there exists f .E. ITRx12 such that, for t .E. TSRx12[5. NND), g(t) = 1 if and only if f(t - 5) = 0, f(t - 4) = 1, f(t - 3) = 1, f(t - 2) = 1,
f(t - 1) = 0;
if and only if
there exists f .E. ITRx12 such that g .E. ERx12(f);
if and only if
g .E. .U.RNG(ERx12). Hence, OTRx12 = .U.RNG(ERx12).
Assignment 1
For the first assignment, each team was told that they were going to play the systems engineering role of system functional analysts and find any functional system design to satisfy the I/O requirement IORx12. Most of the teams, with coaching, eventually found a system isomorphic to the system Zx43 (see MBSE, page 602).
(P.4) Specification of the functional system design (Zx43, 11, TSRx12):
Zx43 = (SZx43, IZx43, OZx43, NZx43, RZx43),
SZx43 = IJS[11, 16],
IZx43 = {0, 1};
OZx43 = {0, 1},
NZx43 = {((x, p), y): ((x, p), y) .E. (SZx43 >< IZx43) >< SZx43; y
= 11, if x .E. {11, 15} and p = 1; (* Waiting for a 0. *)
= 12, if x .E. SZx43 - {15} and p = 0; (* Received a 0. *)
= 13, if x .E. {12, 16} and p = 1; (* Received 0, 1. *)
= 14, if x = 13 and p = 1; (* Received 0, 1, 1. *)
= 15, if x = 14 and p = 1; (* Received 0, 1, 1, 1. *)
= 16, if x = 15 and p = 0}, (* Received 0, 1, 1, 1, 0. *)
RZx43 = {(x, q): (x, q) .E. SZx43 >< OZx43; q
= 1, if x = 16;
= 0, otherwise}.
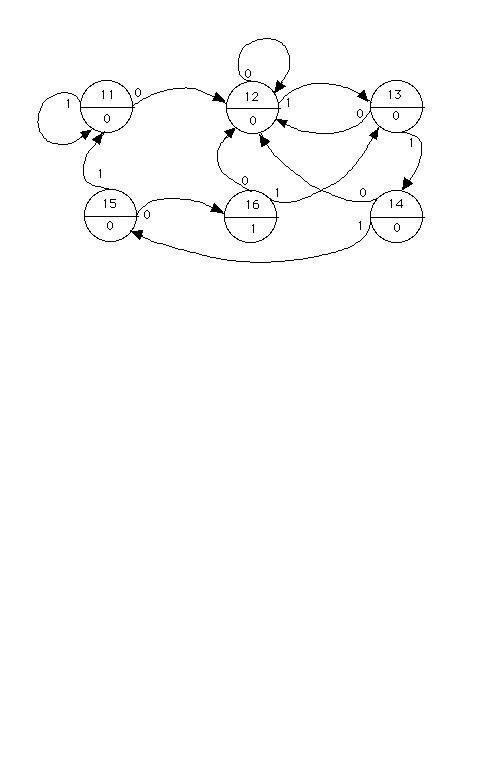
That Zx43 .E. DSYSTEMS, according to the definition at MBSE(2.4), can be verified by inspection.
(P.5) Zx43 satisfies IORx12 completely with respect to the state 11.
Proof:
That (Zx43, 11, TSRx12) .E. FSRx12, that is, that the system Zx43 satisfies IORx12 with respect to the state 11 and the time subscale TSZx43 = TSRx12, is a consequence of the following five deductions/observations corresponding to the conditions required by the definition at MBSE(6.31):
(i) 1 .E. SZx43, by the definition of Zx43.
(ii) TSZx43 = TSRx12 = IJS++ <> {}.
(iii) IZx43 = {0, 1} = IRx12.
(iv) OZx43 = {0, 1} = ORx12.
(v) It must be shown that, if f .E. ITRx12, then OTZx43(f, 11) .E. ERx12(f), since the time subscale of satisfaction is all of TSRx12: OTZx43(f, 11) .E. ERx12(f)
if and only if
for every t .E. TSRx12[5, NND), OTZx43(f, 11)(t) = 1 if and only if f has provided the input stream 0, 1, 1, 1, 0 in the previous 5 time values.
If f .E. ITRx12 and t .E. TSRx12[5, NND), then
OTZx43(f, 11)(t) = 1
if and only if
STZx43(f, 11)(t) = 16,
if and only if
STZx43(f, 11) has, at the times specified in column 1 of the following table, the values specified in one of the columns 2 through 7 (cases A-F - mutually exclusive, collectively exhaustive) and f has the values specified in column 8:
|
Time, s |
STZx43(f, 11)(s), case:
|
f(s) |
| |
A |
B |
C |
D |
E |
F |
|
|
t - 5 |
11 |
12 |
13 |
14 |
15 |
16 |
0 |
|
t - 4 |
12 |
12 |
12 |
12 |
16 |
12 |
1 |
|
t - 3 |
13 |
13 |
13 |
13 |
13 |
13 |
1 |
|
t - 2 |
14 |
14 |
14 |
14 |
14 |
14 |
1 |
|
t - 1 |
15 |
15 |
15 |
15 |
15 |
15 |
0 |
|
t |
16 |
16 |
16 |
16 |
16 |
16 |
|
Hence, STZx43(f, 1)(t) = 16
if and only if
f(t - 5) = 0, f(t - 4) = 1, f(t - 3) = 1, f(t - 2) = 1 and
f(t - 1) = 0.
Therefore, if f .E. ITRx12 and t .E. TSRx12[5, NND), then
OTZx43(f, 11)(t) = 1 if and only if
f(t - 5) = 0, f(t - 4) = 1, f(t - 3) = 1, f(t - 2) = 1 and
f(t - 1) = 0.
Hence OTZx43(f, 1) .E. ERx12(f).
Hence, Zx43 satisfies IORx12 with respect to 11 and TSRx12.
Assignment 2
The student teams now had to play the systems engineering role of system architects to produce an implementation of Zx43 in TYRx2.
A solution to assignment 2 is asserted at MBSE(7.46): Zx43 is implementable in TYRx2 with respect to the system Zx134 buildable in TYRx2 with respect to the system coupling recipe SCRx10, the primary system mode Zx44 of Zx134 and the mappings HS0, HI0 and HO0 given at MBSE(7.46).
Some teams, using the one hot or brute force methods discussed at MBSE(7.55), found other immediately acceptable solutions Zb, buildable in TYRx2 and implementing Zx43. The solution described at MBSE(7.46) is an example of the one hot method. The one hot method requires one component for each state of the system being implemented, in this case, 6, but usually requires no more interconnections than the state transition diagram has interstate transition arrows. The brute force method needs only 3 components but, in general, every component must be connected to every other component.
Specification of a buildable system design for the implementation of
Zx43
The teams mentioned above learned a lesson very valuable to students: it pays to read the text! Two teams, however, presented a version of the implementation scheme caricatured in the following cartoon:
(P.6) Specification of the buildable system design (Zb1, SCR1):
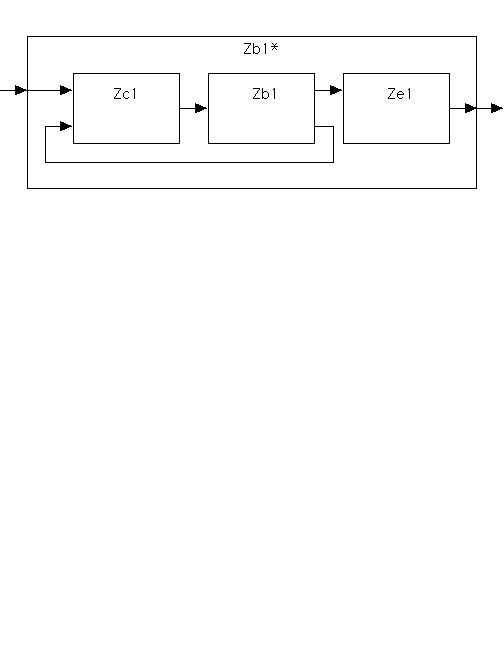
Here, Zb1 = RSY(SCR1) where (* See MBSE(3.3)-(3.11). *)
SCR1 = (VSCR1, CSCR1),
VSCR1 = (Z11,...,Z16), where,
for i .E. IJS[1, 4],
Z1i = (SZ1i, IZ1i, OZ1i, NZ1i, RZ1i),
SZ1i = {0, 1},
IZ1i = {0, 1},
OZ1i = {0, 1} ^ 2,
NZ1i = {((x, p), p): (x, p) .E. SZ1i >< IZ1i},
RZ1i = {(x, (x, x)): x .E. SZ1i},
Z15 = (SZ15, IZ15, OZ15, NZ15, RZ15),
SZ15 = {0, 1},
IZ15 = {0, 1},
OZ15 = {0, 1},
NZ15 = {((x, p), p): (x, p) .E. SZ15 >< IZ15},
RZ15 = {(x, x): x .E. SZ15}
Z16 = (SZ16, IZ16, OZ16, NZ16, RZ16),
SZ16 = {0, 1},
IZ16 = {0, 1} ^ 5,
OZ16 = {0, 1},
NZ16 = {((x, p), y): (x, p) .E. SZ16 >< IZ16; y .E. SZ16; y
= 1, if p = (0, 1, 1, 1, 0);
= 0, otherwise},
RZ16 = {(x, x): x .E. SZ16},
CSCR1 = {(O1Z1i, IiZ16): i .E. IJS[1, 5]}
.U. {(O2Z1i, IZ(i + 1)): i .E. IJS[1, 4]}.
By inspection, Z11,..., Z16 are all in TYRx2, since the only set involved in any state, input or output definition is {0, 1}. SCR1 is a system coupling recipe and, hence, Zb1 is buildable in TYRx2.
Furthermore, by the definition at MBSE(3.47), Zb1 = (SZb1, IZb1, OZb1, NZb1, RZb1),
SZb1 = {0, 1} ^ 6,
IZb1 = {0, 1},
OZb1 = {0, 1},
NZb1 = {((x, p), y): (x, p) .E. SZb1 >< IZb1; y .E. SZb1;
if x = (x1,...,x6) then y = (p, x1, x2, x3, x4, d), where d
= 1, if (x1,..., x5) = (0, 1, 1, 1, 0);
= 0, otherwise},
RZb1 = {(x, x6): x .E. SZb1, x = (x1,...,x6)}.
By the theorem at MBSE(3.62), Zb1 .E. DSYSTEMS.
Does
Zb1 implement Zx43?
(P.7) It is not immediately apparent that Zb1 implements Zx43 as required by the assignment.
The position in which the investigation finds itself at this moment, is, unfortunately, not unusual in industry. Those systems engineers assigned to system functional analysis should choose a functional system design by means of an extensive, detailed, tradeoff study of alternatives within the context of the I/O requirement IOR and the performance requirement PR. That functional system design should be submitted to the systems engineers assigned to system architecture (called physical synthesis in MBSE(1.76)-(1.99)) for implementation. The system architects should choose a buildable system design by means of an extensive, detailed, tradeoff study of alternatives for implementation of the recommended system functional design within the context of the technology requirement TYR and the cost requirement CR. The functional system design together with the buildable system design constitute an implementable system design which should be compared to alternative implementable system designs by means of the tradeoff requirement TR. Instead, the system architects seem frequently to ignore the system functional analysts’ recommendation (if there was one), develop a buildable system design and then begin to "debug" and "integrate" it hoping that their buildable system design can be "evolved" into a system that will satisfy the I/O requirement IOR.
So, typically, it must be asked: What system does Zb1 implement, if any (beside itself)? Clearly, a 1 does not appear at the output port of Zb1 until two time units after the pattern 0, 1, 1, 1, 0 has appeared at the input port, as computations presented in the following table demonstrate for t .E. TSRx12[5, NND):
|
Time |
InputIZb1 |
STZb1 |
OTZb1 |
| |
|
STZ11 |
STZ12 |
STZ13 |
STZ14 |
STZ15 |
STZ16 |
|
|
t - 5 |
0 |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x6 |
|
t - 4 |
1 |
0 |
x1 |
x2 |
x3 |
x4 |
?* |
?* |
|
t - 3 |
1 |
1 |
0 |
x1 |
x2 |
x3 |
? |
? |
|
t - 2 |
1 |
1 |
1 |
0 |
x1 |
x2 |
0 |
0 |
|
t - 1 |
0 |
1 |
1 |
1 |
0 |
x1 |
0 |
0 |
|
t |
p0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
|
t + 1 |
p1 |
p0 |
0 |
1 |
1 |
1 |
1 |
1 |
* At time t - 5, the input to Z16 is (x1,..., x5) which determines the state of Z16 at time t - 4. (x1,..., x5) could be (0, 1, 1, 1, 0) in which case the next state of Z16 would be 1; but if (x1,..., x5) <> (0, 1, 1, 1, 0), then the next state of Z16 would be 0, hence the question mark. At time t - 4, the input to Z16 is (0, x1, x2, x3, x4) which might or might not be (0, 1, 1, 1, 0); hence, the second question mark indicating this uncertainty. But, at time t - 3, the input to Z16 is (1, 0, x1, x2, x3) which could not be (0, 1, 1, 1, 0), so the state of Z16 at time t - 2 is 0. And so for t -1, t and t + 1.
This observation would indicate that there is little chance that Zb1 implements Zx43 with respect to a primary system mode with constant time index 1 (MBSE(5.18)), but try to verify this intuition:
Does
Zb1 implement Zx43 with respect to a primary system mode?
(P.8) In order to show that Zb1 implements Zx43 with respect to any system mode, Zb1m of Zb1, it would be necessary, by the definition at MBSE(5.71), to show that Zx43 is a homomorphic image of Zb1m and hence, in this case, to define a mapping HS from SZb1m onto SZx43 such that HS(NZb1m(x, p)) = NZx43(HS(x), p) and RZb1(x) = RZx43(HS(x)). Since IZb1 = OZb1 = IZx43 = OZx43 = {0, 1}, the input and output homomorphisms, HI and HO, respectively, are both assumed to be the identity, in this case.
Suppose that Zb1m is a primary system mode of Zb1 with system mode behavior function SMBFb1m = {((x, p), (CNSp, 1)): : (x, p) .E. SZb1m}.. Recall that it must be that RZx43(HS(x)) = RZb1m(x), by condition v of the definition of system homomorphism at MBSE(4.3); so the only states of SZb1m that can map onto 16, where RZx43(16) = 1, are those states x such that RZb1m(x) = RZb1(x) = PJN6(x)= 1.
Now at any time t .E. TSZ(0, NND),
OTZb1(f, x)(t)
= RZb1(STZb1(f, x)(t)), by the definition of OTZb1 at MBSE(2.30);
= PJN6(STZb1(f, x)(t)), by the definition of Zb1;
= 1 if and only if PJN(1,..., 5)(STZb1(f, x)(t - 1)) = (0, 1, 1, 1, 0).
Hence, the only states of Zb1m that output 1 are the possible next states after the state (0, 1, 1, 1, 0, 0) and are of the form: (p, 0, 1, 1, 1, 1), where p could be either 0 or 1. Therefore, to establish a homomorphic relation between Zb1m and Zx43 with HS, any state in SZb1m of the form (p, 0, 1, 1, 1, 1) would have to map on 16 .E. SZx43, if they belong to SZb1m - and one or both must belong to SZb1m, else the mapping HS could not be ONTO.
Now try to deduce other elements of HS: Let (X5, 15) .E. HS and x5 = (x51, x52, x53, x54, x55, x56) then,
16
= NZx43(15, 0), by the definition above of Zx43;
= NZx43(HS(x5), 0), where x5 .E. SZb1m and HS(x5) = 15;
= HS(NZb1m(x5, 0)), by condition iv of the definition of system homomorphism at MBSE(4.3);
= HS(NZb1(x5, 0)), by the assumption that Zb1m is primary;
= HS(0, x51, x52, x53, x54, d56), if t = 1 for a primary system mode, where d56 = 1 if and only if x51 = x55 = 0 and x52 = x53 = x54 = 1 and x56 = 0;
= HS(p, 0, 1, 1, 1, 1), for p .E. {0, 1}, because, as pointed out above, the only states of Zb1 that could map onto 16 under HS are of the form (p, 0, 1, 1, 1, 1);
hence, x51 = 0, x52 = x53 = x54 = 1 and d56 = 1, so x55 = 0.
Hence, 15 = HS(0, 1, 1, 1, 0, d) for d .E. {0, 1}. In fact, d has to be 0 because there is no way that the input could provide the pattern 0, 1, 1, 1, 0 and then input a 0 or 1 and get 0, 1, 1, 1, 0 again. Hence,
(HS ^ -1)(15) = {(0, 1, 1, 1, 0, 0)}, there is exactly one state of Zb1 that can map onto 15 under HS and
(HS ^ -1)(16) .S. {(p, 0, 1, 1, 1, 1): p .E. {0, 1}},
Now it must be that: 15
= NZx43(14, 1);
= NZx43(HS(x4), 1), where x4 .E. SZb1m, x4 = (x41,..., x46) and HS(x4) = 14;
= HS(NZb1m(x4, 1)), by condition iv of the definition of system homomorphism at MBSE(4.3);
= HS(1, x41, x42, x43, x44, d46), where d46 = 1 if and only if (x41, x42, x43, x44, x45) = (0, 1, 1, 1, 0);
= HS(0, 1, 1, 1, 0, 0).
This is a contradiction, because, on the one hand, it has been shown that the only state of Zb1 that can map on 15, in a primary system mode, is (0, 1, 1, 1, 0, 0); and, on the other hand, it has been shown that the next state after an input of 1 while in any state that maps on 14 must have its first coordinate equal to 1.
So there is no primary system mode of Zb1 of which Zx43 is a homomorphic image.
The next question is, of course, how about a system mode with time index 2?
This question is left as an exercise for the theoretically inclined student: Prove the following assertion or find a counterexample: Zb1 can not implement Zx43 with respect to a system mode with constant time index d for d < 6. A counterexample would consist of a system mode Zb1m of Zb1 with constant time index d such that 1 < d < 6 of which Zx43 is a homomorphic image. Perhaps a computer program could be written to generate contradictions using the approach above for d = 1.
Does
Zb1 implement any system that satisfies IORx12 with respect to a system mode Zb1m of Zb1 with constant time index 6?
(P.9) No one should have to be doing this, but now, in order to make a point, it is necessary to try to find a system Zx43! that satisfies IORx12 and is a homomorphic image of a system mode Zb1m of Zb1. Zx43 was chosen as the functional system design and Zx43 should have been implemented; instead, it is now necessary to try to make sense of what has been implemented! So what else is new in engineering?
To answer the question: Does Zb1 implement any system that satisfies IORx12 with respect to a system mode Zb1m of Zb1 with constant time index 6, the basic observation is this: The first 5 coordinates of the state of Zb1 can be forced into any desired configuration by time 6 from any state of Zb1 by suitable choice of the input trajectory f, even if f(0) has to be arbitrary (for the purpose of defining a system mode).
Again, start by defining HS. Let SZb1m = {x1,..., x6} such that HS(xi) = 1i for every 1i .E. SZx43. Some limitations on HS have already been discovered. Let x6 = (0, 0, 1, 1, 1, 1) and x5 = (0, 1, 1, 1, 0, 0) from the above discussions. At the other end of the state transition diagram for Zx43, it is clear that the state x1 = (1, 1, 1, 1, 1, 0) could be used to map onto the state 11 because its transition is to itself for any input of 1. Applying an input of 0 to x1 must yield x2 = (0, 1, 1, 1, 1, 0); inputs of 1 to x2 and x3, respectively, must yield x3 = (1, 0, 1, 1, 1, 0) and x4 = (1, 1, 0, 1, 1, 0), respectively. The contradiction established above between the definition of x4 and x5 will not be encountered here because the system mode will have a time index of 6 instead of 1.
There are 32 states x of Zb1 such that PJN6(x) = 1, but only two choices for x6, (0, 0, 1, 1, 1, 1) and (1, 0, 1, 1, 1, 1), because these are the only states x of Zb1 such that PJN6(x) = 1 that are not strictly transient. A transient state is not reachable from any other state and can be encountered in a system experiment data table only as an initial state, such as (0, 0, 0, 0, 0, 1) or (1, 1, 1, 1, 1, 1). All other choices for the xi appear to be arbitrary, limited only by the requirement that the 6th coordinate be 0 so that RZb1m(xi) = RZx43(HS(xi)) = RZx43(i).
Let Zb1m be defined as follows:
SZb1m = {x1,..., x6},
IZb1m = IZb1,
OZb1m = OZb1,
NZb1m
= {((x, p), y): ((x, p), y): .E. (SZb1m >< IZb1m) >< SZb1m; y = STZb1(fxp, x)(txp), where SMBFb1m(x, p) = (fxp, txp)},
RZb1m = RSN(RZb1, SZb1m),
SMBFb1m
= {((x, p), (fxp, txp)):
((x, p), (fxp, txp)): .E. ((SZb1m >< IZb1m) >< (ITZb1, TZb2)); txp = 6;
if x = xi for 1i .E. SZx43 and NZx43(1i, p) = 1j, then fxp = {(0, p), (1, xj5), (2, xj4), (3, xj3), (4, xj2), (5, xj1)}
.U. {(t, 0): t .E. TZb1[6, NND)} where xj = (xj1, xj2, xj3, xj4, xj5, xj6)}.
(P.10) Computation of NZb1m:
|
xi
i= |
p |
f(0) |
f(1) |
f(2) |
f(3) |
f(4) |
f(5) |
NZb1m(x, p)=xj. j= |
|
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
2 |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
2 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
2 |
|
2 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
3 |
|
3 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
2 |
|
3 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
4 |
|
4 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
2 |
|
4 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
5 |
|
5 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
6 |
|
5 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
6 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
2 |
|
6 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
3 |
Now, by the definition of implementation at MBSE(5.71), it must be shown that:
Zb1m .E. DSYSTEMS.
Zb1m is a system mode of Zb1.
Zx43 is a homomorphic image of Zb1m.
(P.11) Zb1m .E. DSYSTEMS.
Proof:
That Zb1m .E. DSYSTEMS is a consequence of the following 5 deductions/observations corresponding to the requirements of the definition of DSYSTEMS at MBSE(2.4):
(i) SZb1m <> {}.
(ii) IZb1m <> {}.
(iii) OZb1m <> {}.
(iv) That NZb1m .E. FNS(SZb1m >< IZb1m, SZb1m) is a consequence of the following 3 deductions/observations required by the definition at MBSE(A1.155):
(i) NZb1m .S. (SZb1m >< IZb1m) >< SZb1m, by definition.
(ii) If (x, p) .E. SZb1m >< IZb1m, then there exists 1i .E. SZx43 such that x = xi, and, since IZb1m = IZx43, there exists 1j .E. SZx43 such that 1j = NZx43(1i, p). Now there is an unique xj .E. SZb1m such that HS(xj) = 1j. It remains to be shown that STZb1(fxp, xi)(6) = xj where fxp = {(0, p), (1, xj5), (2, xj4), (3, xj3), (4, xj2), (5, xj1)}:
| |
Time |
Input |
State |
Output |
| |
0 |
p |
(xi1, xi2, xi3, xi4, xi5, xi6) |
xi6 |
| |
1 |
xj5 |
(p, xi1, xi2, xi3, xi4, ?) |
?1 |
| |
2 |
xj4 |
(xj5, p, xi1, xi2, xi3, ?) |
?2 |
| |
3 |
xj3 |
(xj4, xj5, p, xi1, xi2, ?) |
?3 |
| |
4 |
xj2 |
(xj3, xj4, xj5, p, xi1, ?) |
?4 |
| |
5 |
xj1 |
(xj2, xj3, xj4, xj5, p, ?) |
?5 |
| |
6 |
p’ |
(xj1, xj2, xj3, xj4, xj5, ?) |
?6 |
The ?’s indicate an ambiguity in the output. If i = 6, then xi6 = 1. If i = 5, then ?1 = 1, otherwise all ?1’s are 0. But none of these considerations presents a problem for the present argument, except for ?6; that has to be zero unless j = 6. Now it was shown before that in Zb1, OTZb1(f, x1)(t) = 1 if and only if
STZb1(f, x1)(t - 1) = (0, 1, 1, 1, 0, 0). So, in the above table, ?6 = 1 if and only if (xj2, xj3, xj4, xj5, p, ?) = (0, 1, 1, 1, 0, 0) or xj = (xj1, 0, 1, 1, 1, 0) and p = 0. So xj has to be either x3 or x6. But 13 = NZx43(12, 1) = NZx43(16, 1) and these are the only possibilities for reaching state 13 in Zx43. If p = 0, then xj <> x3. So ?6 = 1 only when xi = x6.
In all cases, ((x, p), xj) .E. NZb1m.
(iii) If (xi’, p’) = (xi’’, p’’), then 1j’ = NZx43(1i’, p’) = NZx43(1i’’. p’’) = 1j’’, so NZb1m(xi’, p’) = NZb1m(xi’’, p’’).
Hence NZb1m .E. FNS(SZb1m >< IZb1m, SZb1m).
(v) RZb1m = PJN6 .E. FNS(SZb1m, OZb1m).
Hence Zb1m .E. DSYSTEMS.
(P.12) Zb1m is a system mode of Zb1.
That Zb1m is a system mode of Zb1 is a consequence of the following 6 deductions/observations corresponding to the conditions required by the definition at MBSE(5.6):
(i) That SMBFb1m .E. FNS(SZb1m >< IZb1m, ITZb1 >< TZb2) is a consequence of the following 3 deductions/observations required by the definition at MBSE(A1.155):
(i) SMBFb1m .S. (SZb1m >< IZb1m) >< (ITZb1 >< TZb2) by the definition of SMBFb1m.
(ii) If (x, p) .E. SZb1m >< IZb1m, then there exists i .E. SZx43 such that x = xi and there exists 1j .E. SZx43 such that 1j = NZx43(1i, p) and hence, ((x, p), (fxp, 6)) .E. SMBFb1m where fxp
= {(0, p), (1, xj5), (2, xj4), (3, xj3), (4, xj2), (5, xj1)}}
.U. {(t, 0): t .E. TZb1[6, NND)}.
(iii) If ((x’, p’), (fx’p’, 6)) .E. SMBFb1m, ((x’’, p’’), (fx’’p’’, 6)) .E. SMBFb1m and (x’, p’) = (x’’, p’’), then there exists 1i .E. SZx43 such that HS(x’) = 1i = HS(x’’), NZx43(1i, p) = 1j .E. SZx43 and fx’p’
= {(0, p), (1, xj5), (2, xj4), (3, xj3), (4, xj2), (5, xj1)}}
.U. {(t, 0): t .E. TZb1[6, NND)}
= fx’’p’’.
Hence, SMBFb1m .E. FNS(SZb1m >< IZb1m, ITZb1 >< TZb2).
(ii) SZb1m = {x1,..., x6} .S. SZb1.
(iii) IZb1m .S. IZb1.
(iv) OZb1m .S. OZb1.
(v) Nzb1m
= {((x, p), y): ((x, p), y): .E. (SZb1m >< IZb1m) >< SZb1m; y = STZb1(fxp, x)(txp), where SMBFb1m(x, p) = (fxp, txp)}.
(vi) RZb1m .S. RZb1.
Hence, Zb1m is a system mode of Zb1.
(P.13) Zx43 is a homomorphic image of Zb1m.
That Zx43 is a homomorphic image of Zb1m is a consequence of the following 5 deductions/observations corresponding to the conditions required by the definition at MBSE(4.3):
(i) HS = {(xi, 1i): 1i .E. SZx43} .E. FNS(SZb1m, 1TO1, ONTO, SZx43).
(ii) ID(IZb1m, IZx43) .E. FNS(IZb1m, 1TO1, ONTO, IZx43).
(iii) ID(OZb1m, OZx43) .E. FNS(OZb1m, 1TO1, ONTO, OZx43).
(iv) If (x, p) .E. SZb1m, IZb1m), x = xi for 1i .E. SZx43, then it must be shown that HS(NZb1f(x, p)) = NZx43(HS(x), p): HS(NZb1f(x, p))
= HS(STZb1(fxp, x)(6)), where SMBFb1m(x, p) = (fxp, 6) and fxp = {(0, p), (1, xj5), (2, xj4), (3, xj3), (4, xj2), (5, xj1)}}
.U. {(t, 0): t .E. TZb1[6, NND)}, if x = xi and NZx43(1i, p) = 1j for {1i, 1j} .S. SZx43, by the definition above for SMBFb1m;
= HS(xj), by the table above computed in the proof that Zb1m is a system;
= 1j, by the definition of HS;
= NZx43(1i, p), by the choice of i1;
= NZx43(HS(xi), ID(p))
as required.
(v) If x .E. SZb1m, it must be shown that RZb1m(x) = RZx43(HS(x)): RZb1m(x)
= RZb1m(xi), if x = xi for 1i .E. SZx43;
= PJN6(xi), by the definition of Zb1 and Zb1m;
= 0, if i <> 6;
= 1, if I = 6;
= RZx43(1i);
= RZx43(HS(xi)).
Hence, Zx43 is a homomorphic image of Zb1m.
Hence Zb1 implements Zx43 with respect to Zb1m, HS, ID and ID..
The problem now is to implement the controller.
(P.14) The system architects who presented Zb1 lucked out after all and implemented Zx43. Six time units must pass in Zb1 for every time unit of IOR. That is, it must be assumed that the system Zb1 runs 6 times faster than the time within which the I/O requirement assumes that the inputs will arrive and the outputs must be produced. So the system architects must use the definition of Zb1m to design and implement a controller Zc1 for Zb1 that will take the inputs specified by IOR in the time scale specified by IOR and the fedback state of Zb1 and produce the appropriate input trajectory for Zb1 that will keep it in the system mode Zb1m while the appropriate output is being computed. And Zc must also be implemented in TYRx2! Ze1 in the following cartoon is an output editor, to be designed so that the output of Zb1* will match the time scale required by IOR. Ze1 must also be implemented in TYRx2. To the contrary, usually, the functions of Zc1 and Ze1 are assigned to human operators.

A general implementation theorem.
The above considerations can be generalized.
(P.15) Theorem: If
{Z1, Z2} .S. DSYSTEMS,
d .E. IJS+,
for every {x, y} .S. SZ1, there exists f .E. ITZ1 such that y = STZ1(f, x)(d),
(* Every state is reachable from every other state in exactly time d. This could be replaced by a hypothesis that every state is reachable from every other state and there exists p0 .E. IZ1 such that NZ1(x, po) = x for every x .E. SZ1. Then take d to be
MAX{MIN{e: y = STZ1(f, x)(e); f .E. ITZ1}: {x, y} .S. SZ1} if the latter is finite. Then, if y = STZ1(f, x)(e) for e < d, simply use STEP(f, e, CNSp0) to satisfy the requirement that y = STZ1(f, x)(d). *)
S .S. SZ1, S <> {},
I .S. IZ1, I <> {},
O .S. OZ1, O <> {},
HS .E. FNS(S, 1TO1, ONTO, SZ2),
HI .E. FNS(I, ONTO, IZ2),
HO .E. FNS(O, ONTO, OZ2),
for every x .E. SZ1, HO(RZ1(x)) = RZ2(HS(x)),
(* To satisfy this requirement, it is necessary that
HO = {(q1, q2): q1 .E. RNG(RSN(RZ1, S)); q2 .E. RNG(RZ2); if x .E. S such that q1 = RZ1(x), then q2 = RZ2(HS(x))}.
If this is not a function, then HS or S must be redefined so that, if RZ1(x1) = RZ1(x2), then RZ2(HS(x1)) = RZ2(HS(x2)). The best choice of S is such that RZ1(x) = x or, at least, so that RSN(RZ1, S) is 1TO1, then the choice of HS is arbitrary as long as it is 1TO1 and ONTO. *)
CHI .E. CHF(ITZ1) and
Z1m = (SZ1m, IZ1m, OZ1m, NZ1m, RZ1m) where
SZ1m = S,
IZ1m = I,
OZ1m = O,
NZ1m = {((x, p), y): {((x, p), y) .E. (SZ1m >< IZ1m) >< SZ1m; y = STZ1(fxp, x)(txp) where SMBF1m(x, p) = (fxp, txp)},
RZ1m = RSN(RZ1, S) and
SMBF1m = {((x, p), (fxp, txp)):
{((x, p), (fxp, txp)) .E. (SZ1m >< IZ1m) >< (ITZ1 >< TZ1+));
if y = (HS ^ -1)(NZ2(HS(x), HI(p))
fxp = CHI({f: f .E. ITZ1; f(0) = p; STZ1(f, x)(d + 1) = y});
txp = d + 1},
(* The time that has to be used is d + 1 because f(0) has to be equal to the last input p and may not be on the input trajectory to take the system from x to y in time d directly, so the input trajectory that has to be used is CTN(CNSp, 1, f’) where f’ is the input trajectory to take the system from NZ1(x, p) to y in time d directly. *)
then
Z1m .E. DSYSTEMS,
Z1m is a system mode of Z1,
Z2 is a homomorphic image of Z1m with respect to HS, HI and HO and
Z1 implements Z2 with respect to Z1m, HS, HI and HO, that is, Z2 = IMPSY(Z1, Z1m, HS, HI, HO) (* See MBSE(5.77). *)
Proof:
That Z2 = IMPSY(Z1, Z1m, HS, HI, HO) is a consequence of the following assertions, corresponding to the conditions required by the definition at MBSE(5.77):
Z1m .E. DSYSTEMS.
Z1m is a system mode of Z1.
Z2 is a homomorphic image of Z1m with respect to HS, HI and HO.
(P.16) Z1m .E. DSYSTEMS.
Proof:
That Z1m .E. DSYSTEMS is a consequence of the following 5 deductions/observations corresponding to the requirements of the definition of DSYSTEMS at MBSE(2.4):
(i) SZ1m = S = DMN(HS) <> {}, because SZ2 <> {} and HS is a function.
(ii) IZ1m = I = DMN(HI) <> {}, because IZ2 <> {} and HI is a function.
(iii) OZ1m = O = DMN(HO) <> {}, because OZ2 <> {} and HO is a function.
(iv) That NZ1m .E. FNS(SZ1m >< IZ1m, SZ1m) is a consequence of the following 3 deductions/observations corresponding to the conditions required by the definition at MBSE(A1.155):
(i) NZ1m .S. (SZ1m >< IZ1m) >< SZ1m, by definition.
(ii) If (x, p) .E. SZ1m >< IZ1m, let SMBF1b(x, p) = (fxp, d + 1) and y = STZ1(fxp, x)(d + 1), then ((x, p), y) .E. NZ1m.
(iii) If (x’, p’) = (x’’, p’’), then (fx’p’, d + 1)
= SMBF1m(x’, p’);
= SMBF1m(x’’, p’’), because SMBF1 is a function; see part (b) below;
= (fx’’p’’, d + 1),
so NZ1m(xi’, p’)
= STZ1(fx’p’, x’)(d + 1), by definition;
= STZ1(fx’’p’’, x’’)(d + 1), because STZ1 is a function and STZ1(f, x) is a function; see below for the former and MBSE(2.29) for the latter;
= NZ1m(xi’’, p’’).
Hence NZ1m .E. FNS(SZ1m >< IZ1m, SZ1m) if STZ1 .E. FNS(ITZ1 >< SZ1, FNS(TZ1, SZ1)), which is proved in the lemma immediately below (inexplicably omitted from MBSE), and SMBF1m .E. FNS(SZ1m >< IZ1m, ITZ1 >< {d + 1}), which is proved below under part (b) of this proof.
Lemma: If Z .E. DSYSTEMS, then STZ .E. FNS(ITZ1 >< SZ1, FNS(TZ1, SZ1)).
Proof: That STZ .E. FNS(ITZ1 >< SZ1, FNS(TZ1, SZ1)) is a consequence of the following three deductions/observations corresponding to the requirements of the definition at MBSE(A1.155)):
(i) As implied by the definition at MBSE(2.27),
STZ = {((f, x), g): (f, x) .E. ITZ >< SZ; g .E. FNS(TZ, SZ); g(0) = x and g(t + 1) = NZ(g(t), f(t)) for every t .E. TZ}.
Hence, STZ .S. (ITZ >< SZ) >< FNS(TZ, SZ).
(ii) If (f, x) .E. ITZ >< SZ,
g = {(t, y): t .E. TZ; y
= x, if t = 0;
= NZ(g(t - 1), f(t - 1), if t <> 0},
then g .E. FNS(TZ, SZ), by the theorem at MBSE(2.29), and ((f, x), g) .E. STZ.
(iii) If {((f’, x’), g’), ((f’’, x’’), g’’)} .S. STZ and , (f’, x’) = (f’’, x’’), then g’(0) = x’ = x’’ = g’’(0). If, for t <> 0 and g’(t) = g’’(t), then g’(t + 1)
= NZ(g’(t), f(t));
= NZ(g’’(t), f(t)), because NZ is a function by the definition at MBSE(2.4);
= g’’(t + 1).
Hence g’ = g’’ and STZ is single-valued.
Hence, STZ .E. FNS(ITZ1 >< SZ1, FNS(TZ1, SZ1)).
(v) RZ1m = RSN(RZ1, SZ1m) .E. FNS(SZ1m, OZ1m).
Hence Z1m .E. DSYSTEMS.
(P.17) Z1m is a system mode of Z1.
Proof:
That Z1m is a system mode of Z1 is a consequence of the following 6 deductions/observations corresponding to the conditions required by the definition at MBSE(5.6):
(i) That SMBF1m .E. FNS(SZ1m >< IZ1m, ITZ1 >< TZ1+) is a consequence of the following 3 deductions/observations required by the definition at MBSE(A1.155):
(i) SMBF1m .S. (SZ1m >< IZ1m) >< (ITZ1 >< TZ1+) by the definition of SMBF1m.
(ii) If (x, p) .E. SZ1m >< IZ1m, x’ = NZ1(x, p) and
y = (HS ^ -1)(NZ2(HS(x), HI(p)), y exists uniquely because HS is 1TO1, then, by hypothesis, there exists f’ .E. ITZ1 such that y = STZ1(f’, x’)(d). Let f’’ = CTN(CNSp, 1, f’); see the definition at MBSE(A1.290). Then STZ1(f’’, x)(d + 1)
= STZ1(f’’ -> 1, STZ1(f’’, x)(1))(d), by the theorem at MBSE(2.46);
= STZ1(f’’ -> 1, NZ1(x, f’’(0))(d), by the definition of STZ1;
= STZ1(f’, x’)(d), by the definition of f’’ and -> and, by the definition of x’;
= y, by the definition of f’. Hence,
{f: f .E. ITZ1; f(0) = p; STZ1(f, x)(d + 1) = y} <> {}. Let
fxp = CHI({f: f .E. ITZ1; f(0) = p; STZ1(f, x)(d + 1) = y}). Then ((x, p), (fxp, d + 1)) .E. SMBF1m.
(iii) If ((x’, p’), (fx’p’, d + 1)) .E. SMBF1m, ((x’’, p’’), (fx’’p’’, d + 1)) .E. SMBF1m and (x’, p’) = (x’’, p’’), then y’
= (HS ^ -1)(NZ2(HS(x’), HI(p’));
= (HS ^ -1)(NZ2(HS(x’’), HI(p’’)), because HS, HI and NZ2 are single-valued;
= y’’. Then
{f: f .E. ITZ1; f(0) = p’; STZ1(f, x)(d + 1) = y’}
= {f: f .E. ITZ1; f(0) = p’’; STZ1(f, x)(d + 1) = y’’}, so,
fx’p’
= CHI({f: f .E. ITZ1; f(0) = p’; STZ1(f, x)(d + 1) = y’});
= CHI({f: f .E. ITZ1; f(0) = p’’; STZ1(f, x)(d + 1) = y’’}
= fx’’p’’.
Hence, fx’p’ = fx’’p’’, and SMBF1m is single-valued.
Hence, SMBF1m .E. FNS(SZ1m >< IZ1m, ITZ1 >< TZ1+).
(ii) SZ1m = S .S. SZ1.
(iii) IZ1m = I .S. IZ1.
(iv) OZ1m = O .S. OZ1.
(v) NZ1m = {((x, p), y): ((x, p), y): .E. (SZ1m >< IZ1m) >< SZ1m; y = STZ1(fxp, x)(txp), where SMBF1m(x, p) = (fxp, txp)}.
(vi) RZ1m .S. RZ1.
Hence, Z1m is a system mode of Z1.
(P.18) Z2 is a homomorphic image of Z1m.
Proof:
That Z2 is a homomorphic image of Z1m is a consequence of the following 5 deductions/observations corresponding to the conditions required by the definition at MBSE(4.3):
(i) HS = .E. FNS(SZ1m, 1TO1, ONTO, SZ2), by hypothesis.
(ii) HI .E. FNS(IZ1m, ONTO, IZ2), by hypothesis.
(iii) HO .E. FNS(OZ1m, ONTO, OZ2), by hypothesis.
(iv) If (x, p) .E. SZ1m >< IZ1m, then it must be shown that HS(NZ1mf(x, p)) = NZ2(HS(x), HI(p)): HS(NZ1mf(x, p))
= HS(STZ1(fxp, x)(d + 1)), where SMBF1m(x, p) = (fxp, d + 1), by the definition above for SMBF1m;
= HS(y), where y = (HS ^ -1)(NZ2(HS(x), HI(p));
= HS((HS ^ -1)(NZ2(HS(x), HI(p))));
= NZ2(HS(xi), HI(p)),
as required.
(v) If x .E. SZ1m, it must be shown that HO(RZ1m(x)) = RZ2(HS(x)): HO(RZ1m(x))
= HO(RZ1(x)), by the definition of Z1m;
= RZ2(HS(x)), by hypothesis.
Hence, Z2 is a homomorphic image of Z1m.
Hence Z1 implements Z2 with respect to Z1m: Z2 = IMPSY(Z1, Z1m, HS, HI, HO).
Specification of another buildable system design (
Zb2, SCR2)
(P.19) There is a system Zb2, buildable in TYRx2, that implements Zx43 by means of a system mode with constant time index 2: Modify SCR1 to obtain a new system coupling recipe SCR2, by inserting a 1 time unit delay: Z1id = (SZ1id, IZ1id, OZ1id, NZ1id, RZ1id) where
SZ1id = IZ1id = OZ1id = {0, 1}, NZ1id = {((x, p), p): (x, p) .E. SZ1id >< IZ1id},
RZ1id = ID(SZ1id),
after each of Z11,..., Z14 so that the desired behavior satisfying IOR will be exhibited by the resultant Zb2 of SCR2 every two time units. See cartoon of SCR2 and Zb2 below.
Exercise for the student:
Show that Zb2 implements a system Zx43! that satisfies IORx12 with respect to a system mode Zb2m with system mode behavior function SMBFb2m such that SMBFb2m(x, p) = (CNSp, 2) for every (x, p) .E. SZb2m >< IZb2m.
Does Zb2 implement Zx43? See technique below.
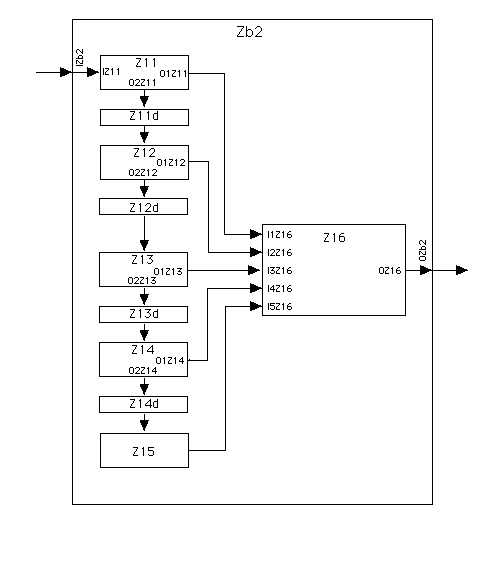
Specification of yet another buildable system design (
Zb3, SCR3)
(P.20) One team must have realized intuitively the limitations of Zb1 and modified Zb1 to avoid its difficulties. Their approach: was to eliminate one component and put the output decision one time unit earlier by providing the input information not only to the first component but also to the fifth component, so that if the fifth component "knows" the states of the other 4 components as well as the input, then the fifth component can output 1 at the time immediately following the completion of the 0, 1, 1, 1, 0 pattern in the input stream.
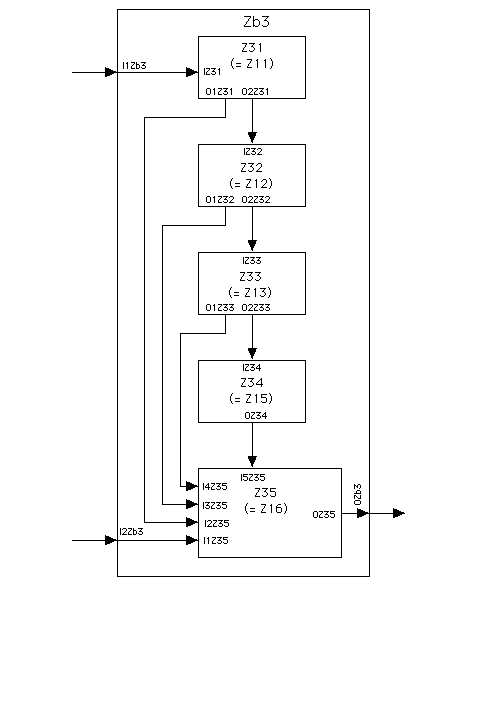
For this system, Zb3 = RSY(SCR3) where
SCR3 = (VSCR3, CSCR3),
VSCR3 = (Z31,..., Z35),
Z3i = Z1i for i .E. IJS[1, 3],
Z34 = Z15,
Z35 = Z16, where Z11,..., Z14 and Z16 are as defined above,
CSCR3 = {(O1Z3i, I(i + 1)Z35): i .E. IJS[1, 3]}
.U. {(OZ34, I5Z35)}
.U. {(O2Z3i, IZ3(i + 1)): i .E. IJS[1, 3]}.
Now, by the definition at MBSE(3.47), Zb3 = (SZb3, IZb3, IZb3, NZb3, RZb3),
SZb3 = {0, 1} ^ 5,
IZb3 = {0, 1} ^ 2,
OZb3 = {0, 1},
NZb3((x1, x2, x3, x4, x5), (p’, p’’))
= (p’, x1, x2, x3, d), where d
= 1, if (p’’, x1, x2, x3, x4) = (0, 1, 1, 1, 0);
= 0, otherwise,
for every (((x1, x2, x3, x4, x5), (p’, p’’)) .E. SZb3 >< IZb3
RZb3(x1,...,x5) = x5, for every (x1,...,x5) .E. SZb3.
Now see how Zb3 behaves when the pattern 0, 1, 1, 1, 0 appears in its input stream, where the input is constrained so that the input to each input port is the same and the initial state is (x1, x2, x3, x4, x5), in terms of the components of Zb3:
|
Time |
Input: IZb3 |
STZb3 |
OTZb3 |
| |
|
STZ31 |
STZ32 |
STZ33 |
STZ34 |
IZ35 |
STZ35 |
|
|
t - 5 |
(0, 0) |
x1 |
x2 |
x3 |
x4 |
(0, x1, x2, x3, x4) |
x5 |
x5 |
|
t - 4 |
(1, 1) |
0 |
x1 |
x2 |
x3 |
(1, 0, x1, x2, x3) |
? |
? |
|
t - 3 |
(1, 1) |
1 |
0 |
x1 |
x2 |
(1, 1, 0, x1, x2) |
0 |
0 |
|
t - 2 |
(1, 1) |
1 |
1 |
0 |
x1 |
(1, 1, 1, 0, x1) |
0 |
0 |
|
t - 1 |
(0, 0) |
1 |
1 |
1 |
0 |
(0, 1, 1, 1, 0) |
0 |
0 |
|
t |
(p0, p0) |
0 |
1 |
1 |
1 |
(p0, 0, 1, 1, 1) |
1 |
1 |
|
t + 1 |
(p1, p1) |
p0 |
0 |
1 |
1 |
(p1, p0, 0, 1, 1) |
0 |
0 |
Suppose (x1,..., x4, x5) = (1, 1, 1, 1, 0) in the above table:
|
Time |
Input: IZb3 |
STZb3 |
OTZb3 |
| |
|
STZ31 |
STZ32 |
STZ33 |
STZ34 |
IZ35 |
STZ35 |
|
|
t - 5 |
(0, 0) |
1 |
1 |
1 |
1 |
(0, 1, 1, 1, 1) |
0 |
0 |
|
t - 4 |
(1, 1) |
0 |
1 |
1 |
1 |
(1, 0, 1, 1, 1) |
0 |
0 |
|
t - 3 |
(1, 1) |
1 |
0 |
1 |
1 |
(1, 1, 0, 1, 1) |
0 |
0 |
|
t - 2 |
(1, 1) |
1 |
1 |
0 |
1 |
(1, 1, 1, 0, 1) |
0 |
0 |
|
t - 1 |
(0, 0) |
1 |
1 |
1 |
0 |
(0, 1, 1, 1, 0) |
0 |
0 |
|
t |
(p0, p0) |
0 |
1 |
1 |
1 |
(p0, 0, 1, 1, 1) |
1 |
1 |
|
t + 1 |
(p1, p1) |
p0 |
0 |
1 |
1 |
(p1, p0, 0, 1, 1) |
0 |
0 |
The state of Zb3 before time t - 5 would have had to have been (1, 1, 0, x4, x5) with input (1, 1).
These computations suggest that Zb3 implements some system Zf1, perhaps not Zx43, that satisfies IORx12. Needed:
The system Zf1 that satisfies IORx12.
Proof that Zf1 satisfies IORx12.
A system mode Zb3m of Zb3.
Proof that Zb3m is a system mode of Zb3.
Proof that Zf1 is a homomorphic image of Zb3m.
(P.21) Specification of Zf1
Zf1 = (SZf1, IZf1, IZf1, NZf1, RZf1),
SZf1 = {0, 1} ^ 5,
IZf1 = {0, 1},
OZf1 = {0, 1},
NZf1(x, p)
= (p, x1, x2, x3, d), where d
= 1, if (p, x1, x2, x3, x4) = (0, 1, 1, 1, 0);
= 0, otherwise,
for every (x, p) .E. SZf1 >< IZf1, x = (x1,...,x5),
RZf1(x) = x5, for every x .E. SZf1, x = (x1,...,x5).
(P.22) Zf1 satisfies IORx12.
Proof:
That Zf1 satisfies IORx12 with respect to the initial state DSZf1 = (1, 1, 1, 1, 0) and TSZf1 = TSRx12 is a consequence of the following 5 deductions/observations corresponding to the conditions required by the definition at MBSE(6.31):
(i) DSZf1 = (1, 1, 1, 1, 0) .E. SZf1.
(ii) TSZf1 .S. TSRx12 and TSRx12 <> {}.
(iii) IZf1 = {0, 1} = IRx12.
(iv) OZf1 = {0, 1} = ORx12.
(v) If f .E. ITRx12, then it will be shown that OTZf1(f, DSZf1) .E. ERx12(f); that is, it will be shown that, for t ≥ 5, OTZf1(f, DSZf1)(t) = 1 if and only if
f(t - 5) = 0, f(t - 4) = 1, f(t - 3) = 1, f(t - 2) = 1, f(t - 1) = 0:
OTZf1(f, DSZf1)(t) = 1 if and only if PJN5(STZf1(f, DSZf1)(t)) = 1 which is true if and only if and the input to Z25 at time t - 1 is (0, 1, 1, 1, 0) which is true if and only if
f(t - 5) = 0, f(t - 4) = 1, f(t - 3) = 1, f(t - 2) = 1, f(t - 1) = 0. See the table above for verification.
Hence, (Zf1, DSZf1, TSZf1) .E. FSRx12, that is, Zf1 satisfies IORx12 with respect to DSZf1 and TSZf1.
(P.23) Specification of Zb3m
Define a system mode Zb3m of Zb3:
Zb3m = (SZb3m, IZb3m, IZb3m, NZb3m, RZb3m),
SZb3m = {0, 1} ^ 5,
IZb3m = {(p, p): p .E. {0, 1}},
OZb3m = {0, 1},
NZb3m((x1,...,x5), (p, p))
= (p, x1, x2, x3, d), where d
= 1, if (p, x1, x2, x3, x4) = (0, 1, 1, 1, 0);
= 0, otherwise,
for every ((x1,...,x5), (p, p)) .E. SZb3m >< IZb3m,
RZb3m(x1,...,x5) = x5, for every (x1,...,x5) .E. SZb3m.
The restriction on the input to Zb3m, that PJN1(p) = PJN2(p), is the only difference between Zb3m and Zb3. Hence, Zb3m .E. DSYSTEMS.
(P.24) Zb3m is a system mode of Zb3.
Proof:
That Zb3m is a system mode of Zb3 with respect to the system mode behavior function SMBFb2m = {((x, p), (CNS(p), 1)): (x, p) .E. SZb3m >< IZb3m} is a consequence of the following 6 deductions/observations corresponding to the conditions required by the definition at MBSE(5.6):
(I) By inspection, SMBFb2m .E. FNS(SZb3m >< IZb3m, ITXb2 >< TZb3+).
(ii) SZb3m = SZb3.
(iii) IZb3m .S. IZb3.
(iv) OZb3m = OZb3.
(v) NZb3(x, p) = STZb3(CNS(p), x)(1) = NZb3m(x, p) for every (x, p) .E. SZb3m >< IZb3m.
(vi) RZb3m(x) = PJN5(x) = RZb3(x) for every x .E. SZb3m.
Hence, Zb3m is a system mode of Zb3.
(P.25) Zf1 is a homomorphic image of Zb3m.
Proof:
That Zf1 is a homomorphic image of Zb3m with respect to
HS = ID(SZb3m),
HI = {((p, p), p): p .E. IZb3m} and
HO = ID(OZb3m),
is a consequence of the following 5 deductions/observations corresponding to the conditions required by the definition at MBSE(4.3):
(i) HS .E. FNS(SZb3m, ONTO, SZf1).
(ii) HI .E. FNS(IZb3m, ONTO, IZf1), by inspection.
(iii) HO .E. FNS(OZb3m, ONTO, OZf1).
(iv) HS(NZb3m(x, (p, p)))
= NZb3m(x, (p, p));
= NZf1(x, p);
= NZf1(HS(x), HI(p, p));
for every (x, (p, p)) .E. SZb3m >< IZb3m.
(v) HO(RZb3m(x))
= RZb3m(x);
= PJN5(x);
= RZf1(x);
= RZf1(HS(x)).
Hence Zf1 is a homomorphic image of Zb3m and, therefore, by the definition at MBSE(5.71), Zb3 implements Zf1 because Zb3m is a system mode of Zb3 of which Zf1 is a homomorphic image.
(P.26) Zb3 also implements Zx43!
So a system Zf1 was implemented that satisfies the I/O requirement, but did the system architects implement the original Zx43? The easiest way to explore this question is to use the implementation transitivity theorem at MBSE(5.97) which says that if a system Z1 is implemented by a system Z2 and Z2 is implemented by a system Z3, then Z1 is implemented by Z3 and deduces the necessary system modes and mappings.
(P.27) Specification of the system mode Zf1m of Zf1.
Try to show that Zf1 implements Zx43, that is, find a system mode Zf1m of Zf1 of which Zx43 is a homomorphic image. Let Zf1m be the reachable system mode of Zf1 generated by the single state DSZf1m where DSZf1m = (1, 1, 1, 1, 0), that is, Zf1m = RSYSMO(Zf1, DSZf1m), see the definition at MBSE(5.23):
SZf1m = {x: x .E. SZf1; there exist f .E. ITZf1 and t .E. TZf1 such that x = STZf1(f, DSZf1m)(t)},
IZf1m = IZf1,
OZf1m = OZf1,
NZf1m(x, p) = NZf1(x, p) for every (x, p) .E. SZf1m >< IZf1m,
RZf1m(x) = RZf1(x), for every x .E. SZf1m.
Zf1m is a primary system mode of Zf1 by the theorem at MBSE(5.20).
(P.28) Specification of the state-homomorphism from Zf1m to Zx43.
Deduce the elements of the set SZf1m and the mapping HS at the same time; check with the state transition diagram of Zx43 above:
|
1
=HS(x1)
x1
=DSZf1m
=NZf1m(x5,1) |
2
=HS(x2)
x2
=NZf1m(xi,0)
i.E.{1,2,3,4,6} |
3
=HS(x3)
x3
=NZ2fm(x2,1)=NZf1m(x6,1) |
4
=HS(x4)
x4
=NZf1m(x3,1) |
5
=HS(x5)
x5
=NZf1m(x4,1) |
6
=HS(x6)
x6
=NZf1m(x5,0) |
| |
|
|
|
|
|
|
(1,1,1,1,0) |
(0,1,1,1,0) |
(1,0,1,1,0) |
(1,1,0,1,0) |
(1,1,1,0,0) |
(0,1,1,1,1) |
| |
(0,0,1,1,0) |
(1,0,0,1,0) |
(1,1,0,0,0) |
|
|
| |
(0,0,0,1,0) |
(1,0,0,0,0) |
|
|
|
| |
(0,0,0,0,0) |
(1,0,1,0,0) |
|
|
|
| |
(0,1,0,1,0) |
|
|
|
|
| |
(0,1,0,0,0) |
|
|
|
|
| |
(0,1,1,0,0) |
|
|
|
|
| |
(0,0,1,0,0) |
|
|
|
|
#(SZf1m) = 17. For every x .E. SZf1m, as entered in the above table, NZf1m(x, 0) and NZf1m(x, 1) are also to be found in the table. The table also shows that HS(NZf1m(x, p)) = NZx43(HS(x), p) = NZx43(HS(x), HI(p)). By inspection of the table it can also be seen that HO(RZf1m(x)) = RZf1m(x) = PJN5(x) = RZx43(HS(x)), for every x .E. SZf1m.
Hence, Zx43 is a homomorphic image of Zf1m, a system mode of Zf1; so Zx43 is implemented by Zf1. But Zf1 is implemented by Zb3 with respect to its system mode Zb3m. Hence Zx43 is implemented by Zb3, by the transitivity of implementation theorem at MBSE(5.97).
What’s going on here system theoretically?
So Zb3 implements Zx43, after all. In fact, Zb1 and Zb2 also implement Zx43. The system architects fell into it and didn’t know it. But was it dumb luck? Or will it happen every time? Is the system architects’ attitude correct, after all? That is, all that must be done is to produce any system that satisfies the I/O requirement and that system will implement whatever functional system design that systems functional analysts may have specified?
(P.29) A buildable system that implements one functional system design, implements all functional system designs: not!
The answer to the last question in full generality is clearly negative: That is, the following assertion is false: if
IOR is an I/O requirement,
(Zf’, DSZf’, TSZf’) and (Zf’’, DSZf’’, TSZf’’) are functional system designs for IOR’ such that TSZf’ = TSZf’‘ = TSR,
TYR is a technology,
ISD’ is an implementable system design for IOR and TYR where
ISD’ = (Zf’, DSZf’, TSZf’, Zb’, SCR’,
Zb’m, HS’, ID(SZb’m), ID(IZb’m)),
then
Zb’ implements Zf’‘ also, that is,
ISD’’ = (Zf’’, DSZf’’, TSZf’’, Zb’, SCR’, Zb’’m, HS’’, ID(SZb’’m), ID(IZb’’m)), is an implementable system design for some system mode Zb’’m of Zb’ and state-homomorphism HS’’.
Here is one of the simplest counterexamples:
Let IORx71 = NORMIO({Zx2, Zx4}, {(Zx2, 2), (Zx4, 2)}, NND, FNS(IJS++, {0, 1})),
where, for i .E. {2, 4}, Zxi = (SZxi, IZxi, OZxi, NZxi, RZxi),
SZxi = {1, 2}, IZxi= {3, 4}, OZxi = {5, 6}, RZxi = {(1, 5), (2, 6)},
NZx2 = {((1, 3), 1), ((1, 4), 1), ((2, 3), 1), ((2, 4), 1)} and
NZx4 = {((1, 3), 2), ((1, 4), 2), ((2, 3), 1), ((2, 4), 1)}. See MBSE, page 591.
For Zx2, there are only two possible output trajectories: OTZx2(f, 1) = CNS5, OTZx2(f, 2) = CTN(CNS6, 1, CNS5). The output trajectory of Zx2 is 5 or 6 at time 0 and constant and equal to 5 after that - independent of f.
For Zx4, there are only two possible output trajectories: OTZx4(f, 1)(t)
= 5, if t = 0 or t .E. TZx4 and t is even;
= 6, if t .E. TZx4 and t is odd, and
OTZx4(f, 2) = OTZx4(f, 1) -> 1.
The output trajectory of Zx4 is a flip-flop of 5’s and 6’s depending only on the initial state: if the initial state is 1 then the output pattern is 565656...; if the initial state is 2, then the output pattern is 656565.... - independent of f.
Since IORx71 = NORMIO({Zx2, Zx4}, {(Zx2, 2), (Zx4, 2)}, NND, FNS(IJS++, {0, 1})), IORx71 = {OLRx71, IRx71, ITRx71, ORx71, OTRx71, ERx71) where
OLRx71 = NND (* TSRx71 = IJS++. *),
IRx71 = {3, 4}, ORx71 = {5, 6},
ITRx71 = FNS(TSRx71, IRx71),
OTRx71 = {OTZx2(CNS3, 2), OTZx4(CNS3, 2)},
ERx71 = {(f, OTRx71): f. E. ITRx71}.
According to the theorem at MBSE(6.47), (Zx2, 2, TSRx71) and (Zx4, 2, TSRx71) are both functional system designs for IORx71.
Let the technology TYR$ consist of all those systems which are exact copies of Zx2. Now, let (Zb$, SCR$) be a buildable system design for TYR$. Suppose, for n .E. IJS+, VSCR$ = (Z$1,..., Z$n), where every Z$i is an exact copy of Zx2 for every i .E. IJS[1, n], then, regardless of the connectivity CSCR$, suppose, for m .E. IJS[1, n), there are m unconnected output ports of SCR$, that is, IZb$ = {3, 4} ^ m. Then, for any input trajectory f for Zb$, and initial state x for Zb$, the output trajectory will produce some m-dimensional subvector of x consisting of 5’s and 6’s at time 0 and then a constant vector of m 5’s after that. Any system mode Zb$m of Zb$ will have exactly the same properties. Hence, Zx4 cannot be implemented in TYR$, but Zx2 is its own implementation in TYR$! So here is the desired counterexample: a case in which an implementation of one functional system design does not implement another functional system design.
There must be an even simpler counterexample! But it has to have the same ingredients, IOR, TYR, FSD1, a functional system design for IOR, ISD1 that implements FSD1 in TYR and FSD2, another functional system design for IOR that is not implemented by ISD1, or, even stronger, is unimplementable in TYR - and proofs of all these relationships or lack thereof.
I/O Equivalence with respect to initial states.
The phenomenon exhibited by the students’ responses was even more limited than the counterexample presented above. There, the two functional system designs had different output trajectories as did their implementations. In the students’ responses both the system functional designs and their implementations produced identical output trajectories. Both the system functional designs (and their implementations) are I/O equivalent in the sense of the next definition.
(P.30) Definition of I/O equivalence with respect to initial states:
Two systems Z1 and Z2 are I/O equivalent with respect to DSZ1 and DSZ2 if and only if
(I) IZ1 = IZ2,
(ii) OZ1 = OZ2,
(iii) DSZ1 .E. SZ1,
(iv) DSZ2 .E. SZ2,
(v) for every f .E. ITZ1 = ITZ2, OTZ1(f, DSZ1) = OTZ2(f, DSZ2) and
(vi) for i .E. {1, 2}, every state of Zi is reachable from DSZi.
(P.31) Corollary: I/O equivalence with respect to initial states is reflexive, symmetric and transitive.
If {Z1, Z2, Z3} .S. DSYSTEMS,
then
Z1 is I/O equivalent to Z1 with respect to DSZ1 for any DSZ1 .E. SZ1 (reflexivity),
if Z1 is I/O equivalent to Z2 with respect to DSZ1 and DSZ2, respectively, then Z2 is I/O equivalent to Z1 with respect to DSZ2 and DSZ1, respectively (symmetry),
if Z1 is I/O equivalent to Z2 with respect to DSZ1 and DSZ2, respectively, and Z2 is I/O equivalent to Z3 with respect to DSZ2 and DSZ3, respectively, then Z1 is I/O equivalent to Z3 with respect to DSZ1 and DSZ3, respectively (transitivity).
State-homomorphisms.
The idea of a state-homomorphism has already been used, but the following definition is written to make the notion precise.
(P.32) Definition of state-homomorphic image
The system Z1 is a state-homomorphic image of the system Z2 with respect to HS if and only if Z1 = HIMSY(Z2, HS, ID(IZ2), ID(OZ2)).
(P.33) Corollary: State-homomorphism implies identical input sets and identical output sets.
Proof: If Z1 = HIMSY(Z2, HS, ID(IZ2), ID(OZ2)), then IZ1 = IZ2 and OZ1 = OZ2.
State-homomorphism implies I/O equivalence with respect to initial states.
(P.34) Theorem: If
{Z1, Z2} .S. DSYSTEMS,
Z1 is a state-homomorph of Z2 with respect to HS,
for i .E. {1, 2}, DSZi .E. SZi such that
every state of Zi is reachable from DSZi and
HS(DSZ2) = DSZ1,
then
Z1 and Z2 are I/O equivalent with respect to DSZ1 and DSZ2.
Proof:
All conditions required by the definition of I/O equivalence with respect to initial states at (P.30) above are fulfilled by the hypotheses except (v), proved as follows:
If f .E. ITZ1 = ITZ2, then OTZ2(f, DSZ2)
= HO o OTZ2(f, DSZ2), since HO = ID(OZ2);
= OTZ1(HI o f, HS(DSZ2)), by the theorem at MBSE(4.22);
= OTZ1(f, DSZ1), since HI = ID(IZ2) and HS(DSZ2) = DSZ1.
Two systems I/O equivalent with respect to initial states implies a homomorphic relationship between the systems: not!
(P.35) To the conjectured Theorem: If
{Z1, Z2} .S. DSYSTEMS and
Z1 and Z2 are I/O equivalent with respect to DSZ1 and DSZ2,
then
Z1 is a state-homomorph of Z2 or Z2 is a state-homomorph of Z1,
there is a counterexample based on the following "near-proof:"
A near proof of the conjectured theorem
Let HS = {(STZ1(f, DSZ1)(t), STZ2(f, DSZ2)(t)): (f, t) .E. ITZ1 >< TSZ1}, as the most "natural" candidate for the definition of the state-homomorphism. Assuming HS .E. FNS(SZ1, ONTO, SZ2):
HS(NZ1(x, p))
= HS(NZ1(STZ1(f, DSZ1)(t), p)), where x = STZ1(f, DSZ1)(t) for some (f, t) .E. ITZ1 >< TSZ1 and it can be assumed that f(t) = p;
= HS(STZ1(f, DSZ1)(t + 1));
= STZ2(f, DSZ2)(t + 1), by the definition of HS;
= NZ2(STZ2(f, DSZ2)(t), f(t));
= NZ2(HS(x), HI(p)) and
HO(RZ1(x))
= RZ1(STZ1(f, DSZ1)(t)), where x = STZ1(f, DSZ1)(t) and because HO = ID(OZ1);
= OTZ1(f, DSZ1)(t);
= OTZ2(f, DSZ2)(t), since Z1 and Z2 are I/O equivalent with respect to DSZ1 and DSZ2;
= RZ2(STZ2(f, DSZ2)(t));
= RZ2(HS(x)).
Now it must be shown that HS .E. FNS(SZ1, ONTO, SZ2) according to the definition at MBSE(A1.155):
(i) HS .S. SZ1 >< SZ2.
(ii) If x .E. SZ1, then, by the reachability hypothesis, there exists (f, t) .E. ITZ1 >< TSZ1 such that x = STZ1(f, DSZ1)(t). Then (x, STZ2(f, DSZ2)(t)) .E. HS.
(iii) Now let STZ1(f1, DSZ1)(t1) = x = STZ1(f2, DSZ1)(t2). Is STZ2(f1, DSZ2)(t1) = y = STZ2(f2, DSZ2)(t2)?
Aye, there’s the rub! HS may not be single-valued. Everything else went through but not necessarily the single-valuedness of HS. On to the counterexample:
The Counterexample
(P.36) Two systems Zx178 and Zx179 will be defined both with state set IJS[1, 4]. It will be shown that neither is a state-homomorphic image of the other.
Then a third system Zx180 will be defined with state set {a, b, c} and it will be shown that Zx180 is a state-homomorphic image of both Zx178 and Zx179, with respect to mappings HS1 and HS2, respectively. It will be seen that HS1(1) = HS2(1) = a, and hence, by the theorem proved at (P.34) above, Zx178 is I/O equivalent to Zx180 with respect to 1 and a, and Zx179 is I/O equivalent with respect to 1 and a and hence, by the symmetry and transitivity of I/O equivalence asserted at (P.31), Zx178 and Zx179 are I/O equivalent with respect to the initial states 1 and 1, respectively.
Hence, it is not the case that I/O equivalence with respect to initial states between two systems implies a state-homomorphism between the systems.
Specification of
Zx178 and Zx179.
(P.37) Let:
Zx178 = (SZx178, IZx178, OZx178, NZx178, RZx178) where
SZx178 = {1, 2, 3, 4},
IZx178 = {1, 2, 3},
OZx178 = {1, 2, 3},
NZx178 = {((1, 1), 2), ((1, 2), 3), ((1, 3), 1),
((2, 1), 3), ((2, 2), 3), ((2, 3), 1),
((3, 1), 2), ((3 2), 4), ((3, 3), 1),
((4, 1), 3), ((4 2), 3), ((4, 3), 1)},
RZx178 = {(1, 1), (2, 2), (3, 3), (4, 2)},

and Zx179 = (SZx179, IZx179, OZx179, NZx179, RZx179) where
SZx179 = {1, 2, 3, 4},
IZx179 = {1, 2, 3},
OZx179 = {1, 2, 3},
NZx179 = {((1, 1), 2), ((1, 2), 3), ((1, 3), 1),
((2, 1), 3), ((2, 2), 4), ((2, 3), 1),
((3, 1), 2), ((3 2), 2), ((3, 3), 1),
((4, 1), 2), ((4 2), 2), ((4, 3), 1)},
RZx179 = {(1, 1), (2, 2), (3, 3), (4, 3)}.

By inspection, {Zx178, Zx179} .S. DSYSTEMS, according to the definition at MBSE(2.4).
There is no state-homomorphism between
Zx178 and Zx179.
(P.38) If HS
= {(STZx178(f, DSZx178)(t), STZx179(f, DSZx179)(t)):
(f, t) .E. ITZx178} >< TSZx178},
where DSZx178 = DSZx179 = 1, then HS is not single-valued: 3 = STZx178(CNS2, 1)(1) = STZx178(CNS2, 1)(3), but STZx179(CNS2, 1)(1) = 3 <> 4 = STZx179(CNS2, 1)(3).
But what about some other definition for HS? The necessity to have HO1(RZx178(x)) = RZx179(HS1(x)) where, in this case, HO1 = ID, implies that HS1 = {(1, 1), (2, 2), (3, 3), (4, 2)}, which is single-valued but not ONTO, or else HS1 = {(1, 1), (2, 2), (3, 3), (4, 2), (3, 4)}, which is ONTO but not single-valued. It must be concluded that Zx179 is not a state-homomorphic image of Zx178. The same problems arise in trying to define HS2 in order for Zx178 to be a state-homomorphic image of Zx179: Either HS2 = {(1, 1), (2, 2), (3, 3), (4, 3)}, which is single-valued but not ONTO, or
HS2 = {(1, 1), (2, 2), (3, 3), (4, 3), (2, 4)}, which is ONTO but not single-valued. So Zx178 is not a state-homomorphic image of Zx179.
Specification of
Zx180.
(P.39) Let Zx180 = (SZx180, IZx180, OZx180, NZx180, RZx180) where
SZx180 = {a, b, c},
IZx180 = {1, 2, 3},
OZx180 = {1, 2, 3},
NZx180 = {((a, 1), b), ((a, 2), c), ((a, 3), a),
((b, 1), c), ((b, 2), c), ((b, 3), a),
((c, 1), b), ((c 2), b), ((c, 3), a)},
RZx180 = {(a, 1), (b, 2), (c, 3)},

By inspection, Zx180 .E. DSYSTEMS, according to the definition at MBSE(2.4).
Zx180 is a state-homomorphic image of both Zx178 and Zx179.
(P.40) Let HS1 = {(1, a), (2, b), (3, c), (4, b)}. The following table shows the results of computations proving that HS1(NZx178(x, p)) = NZx180(HS1(x), p) (same row entries in columns 4 and 5 are identical) and RZx178(x) = RZx180(HS1(x)) (same row entries in columns 6 and 7 are identical) for every x .E. SZx178 and p .E. IZx178.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
State
x |
Input
p |
NZx178(x, p) |
HS1(NZx178(x, p)) |
NZx180(HS1(x), p) |
RZx178(x) |
RZx180(HS1(x)) |
|
1 |
1 |
2 |
b |
b |
1 |
1 |
|
1 |
2 |
3 |
c |
c |
|
|
|
1 |
3 |
1 |
a |
a |
|
|
|
2 |
1 |
3 |
c |
c |
2 |
2 |
|
2 |
2 |
3 |
c |
c |
|
|
|
2 |
3 |
1 |
a |
a |
|
|
|
3 |
1 |
2 |
b |
b |
3 |
3 |
|
3 |
2 |
4 |
b |
b |
|
|
|
3 |
3 |
1 |
a |
a |
|
|
|
4 |
1 |
3 |
c |
c |
2 |
2 |
|
4 |
2 |
3 |
c |
c |
|
|
|
4 |
3 |
1 |
a |
a |
|
|
Let HS2 = {(1, a), (2, b), (3, c), (4, c)}. The following table shows the results of computations proving that HS2(NZx179(x, p)) = NZx180(HS2(x), p) (same row entries in columns 4 and 5 are identical) and RZx179(x) = RZx180(HS2(x)) (same row entries in columns 6 and 7 are identical) for every x .E. SZx179 and p .E. IZx179.
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
State
x |
Input
p |
NZx179(x, p) |
HS2(NZx179(x, p)) |
NZx180(HS2(x), p) |
RZx179(x) |
RZx180(HS2(x)) |
|
1 |
1 |
2 |
b |
b |
1 |
1 |
|
1 |
2 |
3 |
c |
c |
|
|
|
1 |
3 |
1 |
a |
a |
|
|
|
2 |
1 |
3 |
c |
c |
2 |
2 |
|
2 |
2 |
4 |
c |
c |
|
|
|
2 |
3 |
1 |
a |
a |
|
|
|
3 |
1 |
2 |
b |
b |
3 |
3 |
|
3 |
2 |
2 |
b |
b |
|
|
|
3 |
3 |
1 |
a |
a |
|
|
|
4 |
1 |
2 |
b |
b |
3 |
3 |
|
4 |
2 |
2 |
b |
b |
|
|
|
4 |
3 |
1 |
a |
a |
|
|
Hence, Zx180 is a state-homomorphic image of both Zx178 and Zx179 with respect to HS1 and HS2, respectively. Every state of Zx180 is reachable from the state a .E. SZx180 and every state of both Zx178 and Zx179 is reachable from the state 1 .E. SZx178 .I. SZx179. Furthermore, HS1(1) = HS2(1) = a. So, according to the theorem at (P.34), Zx178 and Zx179 are both I/O equivalent to Zx180 with respect to the initial states 1 and a in both cases. By the symmetry and transitivity of I/O equivalence with respect to initial states as asserted in the corollary to the definition of I/O equivalence with respect to initial states (P.31), Zx178 and Zx179 are I/O equivalent with respect to the states 1 .E. SZx178 and 1 .E. SZx179. But neither Zx178 nor Zx179 is a state-homomorphic image of the other.
Assumption of reusability may be dangerous
(P.41) The practical implication of such a possibility can be seen from the following scenario:
System functional analysts in systems engineering specify that Zx178 shall be implemented.
Zx179 is actually implemented by system architects in systems engineering with a buildable system Zb$. That’s OK, isn’t it?: After all, Zx178 and Zx179 are I/O equivalent with respect to initial states and, furthermore, if Zx178 or Zx179 is implemented, then Zx180 is automatically implemented. So what difference does it make which of Zx178 or Zx179 is implemented?
Later, in the same or another project, systems engineering discovers that a certain function can be performed by Zx178 started in state 4. Wanting to reuse whatever they can and thinking that Zx178 is implemented by Zb, systems engineering specifies Zb$ and the system fails because Zx178 and Zx179 are not I/O equivalent with respect to the states 4.
What can be said about two systems Z1 and Z2 that are I/O equivalent with respect to initial states is that for each system there is another system Z1* and Z2*, respectively, which is a state-homomorphic image of Z1 and Z2 respectively, and Z1* and Z2* are state-isomorphic, or essentially the same system.
I/O Equivalence and Minimality.
(P.42) Definition : If Z .E. DSYSTEMS and {x, y} .S. SZ, then states x and y are I/O equivalent if and only if OTZ(f, x) = OTZ(f, y) for every f .E. ITZ. The system Z is minimal if and only if Z has no I/O equivalent states.
Examples of minimal systems.
(P.43) Zx43 is minimal; Zx180 is minimal
Proof:
Zx43 is minimal because for every {x, y} .S. SZx43, the table at (P.5) above shows that there exists f .E. ITZx43 and t .E. TZx43 such that OTZx43(f, x)(t) <> OTZx43(f, y)(t).
For example, the table at (P.5) shows that state 11 is not I/O equivalent to state 12 since, if f(0), f(1), f(2) and f(3) have the values, respectively, 1, 1, 1, 0, then OTZx43(f, 11)(4) = 0 <> 1 = OTZx43(f, 12)(4).
Similarly, 11 is not I/O equivalent to any of the other states in IJS[12, 15].
State 12 is not I/O equivalent to state 13, for example, since if f provides initially the string of inputs 1, 1, 0, then OTZx43(f, 12)(3) = 0 <> 1 = OTZx43(f, 13)(3).
Hence, none of the states in IJS[11, 15] is I/O equivalent to any other state in IJS[11, 15].
None of the states in IJS[11, 15] is equivalent to 6 because a necessary condition for states x and y to be I/O equivalent is that RZx43(x) = RZx43(y), since, otherwise, OTZx43(f, x)(0) = RZx43(x) <> RZx43(y) = OTZx43(f, y)(0).
Hence, Zx43 is minimal.
The system Zx180 is minimal since RZx180(x) <> RZx180(y) for every {x, y} .S. SZx180, x <> y. So SZx180 has no equivalent states and Zx180 is minimal.
Two systems I/O equivalent with respect to initial states have state-isomorphic minimizations.
(P.44) Theorem: If
{Z1, Z2} .S. DSYSTEMS,
Z1 and Z2 are I/O equivalent with respect to DSZ1 and DSZ2,
for i .E. {1, 2},
Zi = RSYSMO(Zi, DSZi),
Zi* = MINSY(Zi), such that DSZi* = EQZi(DSZi),
then
Z1* is state-isomorphic to Z2*.
Proof:
First, by the theorem at (3.5.126) in MINSY/MAXSYDraft, Zi and Zi* are I/O equivalent with respect to DSZi and DSZi*. By hypothesis, Z1 and Z2 are I/O equivalent with respect to DSZ1 and DSZ2. By the symmetry and transitivity of I/O equivalence, Z1* and Z2* are I/O equivalent with respect to DSZ1* and DSZ2*.
It must be shown that there exists HS .E. FNS(SZ1*, 1TO1, ONTO, SZ2*) such that for (x, p) .E. SZ1* >< IZ1*, HS(NZ1*(x, p)) = NZ2*(HS(x), p) and HO(RZ1*(x)) = RZ2*(HS(x)).
Let HS = {(STZ1*(f, DSZ1*)(t), STZ2*(f, DSZ2*)(t)): (f, t) .E. ITZ1* >< TSZ1*}, as the most "natural" candidate for the definition of the state-isomorphism. Assuming HS .E. FNS(SZ1*, 1TO1, ONTO, SZ2*): for (x, p) .E. SZ1* >< IZ1*,
HS(NZ1*(x, p))
= HS(NZ1*(STZ1*(f, DSZ1*)(t), p)), where x = STZ1*(f, DSZ1*)(t) for some (f, t) .E. ITZ1* >< TSZ1* where it can be assumed that f(t) = p, if f(t) <> p, use f’ = CTN(f, t, CNSp);
= HS(STZ1*(f, DSZ1*)(t + 1)), by the definition at MBSE(2.27);
= STZ2*(f, DSZ2*)(t + 1), by the definition of HS;
= NZ2*(STZ2*(f, DSZ2*)(t), f(t));
= NZ2*(HS(x), p) and
RZ1*(x)
= RZ1*(STZ1*(f, DSZ1*)(t)), where x = STZ1*(f, DSZ1*)(t);
= OTZ1*(f, DSZ1*)(t);
= OTZ2*(f, DSZ2*)(t), since Z1* and Z2* are I/O equivalent with respect to DSZ1* and DSZ2*;
= RZ2*(STZ2*(f, DSZ2*)(t));
= RZ2*(HS(x)).
Now all that must be shown is that HS .E. FNS(SZ1*, 1TO1, ONTO, SZ2*). That HS .E. FNS(SZ1*, SZ2*) is a consequence of the following three observations/deductions corresponding to the conditions required by the definition at MBSE(A1.155):
(i) HS .S. SZ1* >< SZ2*.
(ii) If x .E. SZ1*, then, by the reachability hypothesis, there exists (f, t) .E. ITZ1* >< TSZ1* such that x = STZ1*(f, DSZ1*)(t). Then (x, STZ2*(f, DSZ2*)(t)) .E. HS.
(iii) Now it must be shown that HS is single-valued; let STZ1*(f1, DSZ1*)(t1) = x = STZ1*(f2, DSZ1*)(t2). It must be shown that, if y1 = STZ2*(f1, DSZ2*)(t1) and y2 = STZ2*(f2, DSZ2*)(t2), then y1 = y2.
Z2* is minimal, by hypothesis, and therefore, Z2* has no two I/O equivalent states, by the definition at (3.5.106) in MINSY/MAXSYDraft.. If it can be shown, therefore, that y1 and y2 are I/O equivalent, then it can be concluded that y1 = y2. To this end, it must be shown that for every f .E. ITZ2*, OTZ2*(f, y1) = OTZ2*(f, y2).
Let f .E. ITZ2* and t .E. TZ2* be arbitrary. It will be shown that OTZ2*(f, y1)(t) = OTZ2*(f, y2)(t). Let f’ = CTN(f1, t1, f) and f’’ = CTN(f2, t2, f), then f’ -> t1 = f’’ -> t2 = f, by the theorem at MBSE(A1.297). Note that x
= STZ1*(f’, DSZ1*)(t1);
= STZ1*(f’’, DSZ1*)(t2),
y1 = STZ2*(f’, DSZ2)(t1) and y2 = STZ2*(f’’, DSZ2*)(t2), as consequences of the theorem at MBSE(2.48).
Then OTZ2*(f, y1)(t)
= RZ2*(STZ2*(f, STZ2*(f1, DSZ2*)(t1))(t)), by the definition of y1 and of OTZ at MBSE(2.30);
= RZ2*(STZ2*(f’, DSZ2*)(t1 + t)), by the theorem at MBSE(2.138);
= OTZ2*(f’, DSZ2*)(t1 + t);
= OTZ1*(f’, DSZ1*)(t1 + t), since Z2* and Z1* are I/O equivalent with respect to DSZ2* and DSZ1*, as proved in the first paragraph of this proof;
= RZ1*(STZ1*(f’, DSZ1*)(t1 + t));
= RZ1*(STZ1*(f’ -> t1, STZ1*(f’, DSZ1*)(t1))(t)), by the theorem at MBSE(2.46);
= RZ1*(STZ1*(f, STZ1*(f1, DSZ1*)(t1))(t));
= RZ1*(STZ1*(f, x)(t));
= RZ1*(STZ1*(f, STZ1*(f2, DSZ1*)(t2))(t)), by hypothesis;
= RZ1*(STZ1*(f’’, DSZ1*)(t2 + t), by the definition of f’’ and the theorem at MBSE(2,138);
= OTZ1*(f’’, DSZ1*)(t2 + t);
= OTZ2*(f’’, DSZ2*)(t2 + t), because Z1* and Z2* are I/O equivalent for DSZ1* and DSZ2*;
= RZ2*(STZ2*(f’’ -> t2, STZ2(f’’, DSZ2*)(t2))(t)), by the theorem at MBSE(2.46);
= RZ2*(STZ2*(f, y2)(t));
= OTZ2*(f, y2)(t).
Hence, y1 and y2 are I/O equivalent and, since by hypothesis, Z2* is minimal, y1 = y2, and HS is single-valued.
Hence HS .E. FNS(SZ1*, SZ2*).
HS is ONTO by the reachability hypothesis.
Exactly the same argument used to prove that HS is single-valued can be used to prove that HS is 1TO1 by exchanging the roles of Z1 and Z2.
Hence, Z1* and Z2* are state-isomorphic and Z1* is a homomorphic image of Z1 and Z2* is a homomorphic image of Z2.
Conclusions
It is clear from the definition of implementation at MBSE(5.71) and the transitivity of homomorphism at MBSE(4.31), that, if Z1 implements Z2 and Z3 is a homomorphic image of Z2, then Z1 also implements Z3. The minimization, say Z2*, of a system Z2 is a state-homomorphic image of Z2, so, if Z1 implements Z2, then Z1 also implements Z2*.
Two systems have identical I/O behavior with respect to initial states if and only if they have state-isomorphic minimizations.
But it is also true that two systems may have identical I/O behavior with respect to initial states but neither is a state-homomorphic image of the other. Hence, a system that implements the one may not implement the other. That is, the fact that Z1 is an implementation of Z2* does not imply that Z1 is an implementation of Z2. To assume otherwise can lead to disaster.
It is the responsibility of systems engineers assigned to system functional analysis to consider the I/O requirement and the performance requirement and to specify functional system designs for implementation. It is the responsibility of systems engineers assigned to system architecture to consider the technology requirement and the cost requirement and to specify buildable sysem designs to implement those exact functional system designs.
References
Chapman, W. L., A. T. Bahill and A. W. Wymore, Engineering Modeling and Design, CRC Press, 1992.
[MBSE] Wymore, A. Wayne, Model-Based Systems Engineering, CRC Press, Inc., 2000 Corporate Blvd., N. W., Boca Raton, FL 33431, 1 800 272 7737, 1993.
Author biography
Wayne Wymore
earned BS and MS degrees at Iowa State University, and the PhD at the University of Wisconsin, Madison, all in mathematics. He is Professor Emeritus of Systems and Industrial Engineering at the University of Arizona where he was the first Chairman of the Department of Systems Engineering and first Director of the Computing Center. While managing, teaching, researching and consulting internationally, he authored A Mathematical Theory of Systems Engineering: The Elements, 1967, Systems Engineering Methodology for Interdisciplinary Teams, 1976, and Model-Based Systems Engineering, 1993. System Functional Analysis and System Design, Phase 2 of Model-Based Systems Engineering is forthcoming.
Notation
^ the exponentiation operator MBSE(A1.114), MBSE(A1.115), MBSE(A1.141), MBSE(A1.244), MBSE(A1.406)
^ -1 the inverse function operator MBSE(A1.244)
# the dimension of a vector or the number-of-elements-in-a-set operator MBSE(A1.122), MBSE(A1.236)
* the multiplication operator MBSE(A1.114), MBSE(A1.115), MBSE(A1.201), MBSE(A1.406)
+ the addition operator MBSE(A1.114), MBSE(A1.115), MBSE(A1.201)
- the subtraction, negative and complementation operator MBSE(A1.27), MBSE(A1.114)
-> the translation operator MBSE(A1.284)
.C. the "contains" relation MBSE(A1.3), MBSE(A1.133)
.E. the "is an element of" relation MBSE(A1.2), MBSE(A1.126)
.GE. the greater than or equal to relation for real numbers MBSE(A1.114)
.GT. the greater than relation for real numbers MBSE(A1.114)
.I. the intersection operator MBSE(A1.74), MBSE(A1.85)
.LE. the less than or equal to relation for real numbers MBSE(A1.114).
.LT. the less than relation for real numbers MBSE(A1.114)
.NC. the "does not contain" relation MBSE(A1.3), MBSE(A1.133)
NND infinity MBSE(A1.115), MBSE(A1.236)
.NE. the "is not an element of" relation MBSE(A1.2), MBSE(A1.126)
.NS. the "is not a subset" relation MBSE(A1.3), MBSE(A1.133)
PRD the product operator MBSE(A1.193), MBSE(A1.406)
.PS. the power set operator MBSE(A1.46)
.S. the subset relation MBSE(A1.3), MBSE(A1.133)
SUM the summation operator MBSE(A1.193)
.U. the union operator MBSE(A1.53), MBSE(A1.68)
/ the division operator MBSE(A1.114)
1TO1 the one to one property MBSE(A1.222)
<<>> the "is not equivalent to" relation MBSE(A1.228)
<> the "not equals" relation MBSE(A1.16), MBSE(A1.128), <> is also the equivalence class designator MBSE(A1.383)
= the "equals" relation MBSE(A1.2), MBSE(A1.16), MBSE(A1.128)
== the equivalence relation MBSE(A1.228), MBSE(A1.307)
><
the Cartesian product operator MBSE(A1.141)
o the function composition operator MBSE(A1.269)
{ the first symbol in a set definition by enumeration or extension MBSE(A1.2)
{} the empty set MBSE(A1.39)
} the terminal symbol in a set definition by enumeration or extension MBSE(A1.2)
( the first symbol in a vector definition by enumeration or extension MBSE(A1.122), MBSE(A1.180)
() the empty vector MBSE(A1.122)
) the terminal symbol in a vector definition by enumeration or extension MBSE(A1.122), MBSE(A1.180)







